https://arxiv.org/abs/2402.19302
Introduction
2Dでいうとパズルを埋めて絵を作るように、3DではLEGOをはめるように、1つ1つのピースを組み合わせて本来ある形に復元するというのがSpatial Intelligenceの具体的なタスク例で、視覚-空間世界を正確に知覚し、知覚された空間に対して変換を行う能力らしい。
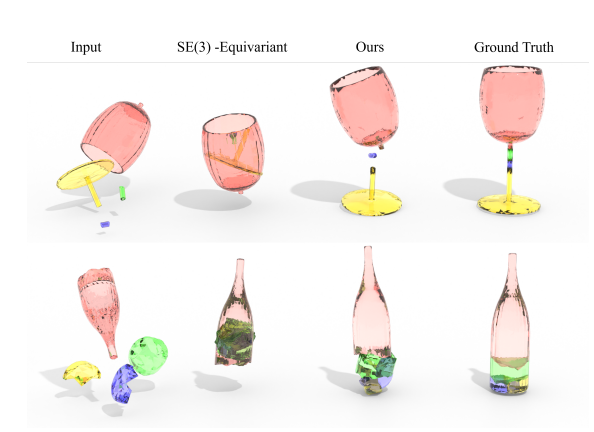
2Dの場合は回転や平行移動の操作を施すことによって、順列問題として扱えて、最適化の手法を用いて解ける。しかし、これはノイズの混入にかなり弱い。直近では最適化のアルゴリズムベースではなく、データ駆動の学習の研究もあるが、回転に対応できないし通常は最適化ベースのアルゴリズムに勝てない。
3Dの場合は3Dのピースは規則的ではないので順列問題として解けず、離散的ではなく連続的な問題として解く必要があり、より難しい。3Dのピースを当てての再構築はまだ2Dほどの性能を出せない。
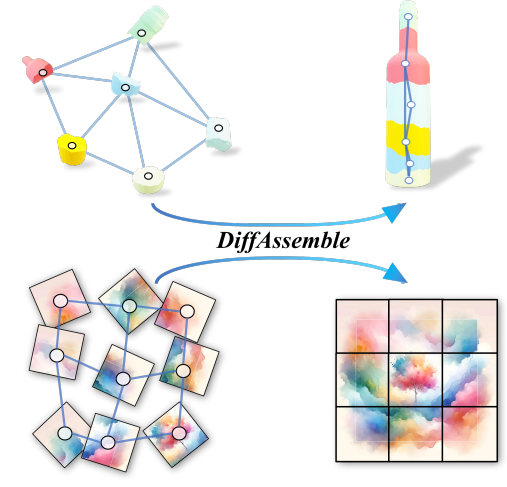
2D, 3Dに共通する考え方として、グラフベースのものを提案する。ピースからの復元はDiffusion Modelを用いて複数ステップを行う。各ピースの持つ情報は本体の外観と位置と向きを持たせるらしい。
最初にユークリッド空間に十分に乱雑となっている条件で、ガウシアンノイズを加えていく。次に、Attention Based Graph Neural Networkを用いて、ノイズ除去の学習を行う。これがDiffAssembleである。
この研究の貢献は以下の3つである。
- 2D, 3Dで同じフレームワークを用いて実現し、SOTAの性能を出す。
- 2D, 3Dでは何が同じで、何が違うかを明らかにする。
- 2Dでの回転と平行移動を適用。
Related Work
- ピースからの復元は、パズルの復元が2D, 3Dともに多い。
- 2Dジグソーパズルでは、人間が作った特徴量に従って、最適化と貪欲法のアルゴリズムベースのものが強い。データ駆動型で学習させたものも性能は及ばないが、不正規入力に強い。
- 3Dでは、具体的にはフレスコ画の復元や家具の組み立てなどで使われている。DNNベースでの解決が主流だが、幾何学的な手掛かりをうまくとらえられてないと思える。
- 拡散確率モデル(Diffusion)は、複雑な分布についての学習をするときの手法の1つである。拡散モデルで対数確率密度を用いて漸化式を組み立てると、その分布の上をうまくサンプリングできることが数学的にわかっている。学習では、うまく対数確率密度を予測するモデルを作ることになる。
- GNNは任意の数の要素や相互関係を記述できるので、空間的な学習が必要なものではよくt買われている。Attention basedのGNN持つkる得るらしい。
Method
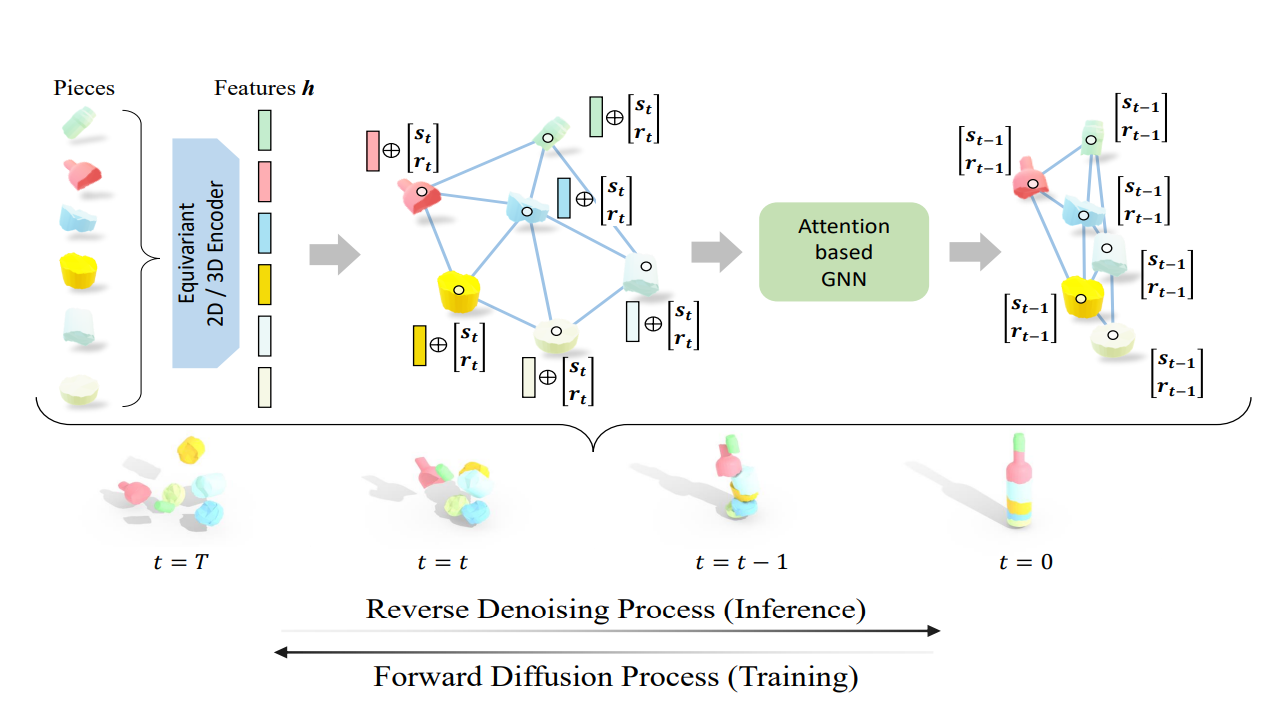
では正しい位置、正しい向きにピースが存在するが、それを徐々にノイズを加えて乱雑にしていく。各タイムステップにおいて、Attention Based GNNは、各ノードのピースの見た目上の特徴とその位置と向きを記述されたグラフを入力として受け取るらしい。
Graph Formulation
合計で個のピースがあり、それぞれがノードにあたる。グラフは完全グラフであり、各ノードには以下のような情報を持たせる。
- ピースの特徴 ベクトル表現である。
- ピースの位置 座標点をそのまま入れており、2Dなら、3Dならである。
- 回転行列 回転している向き
- この行列を表せるようなベクトル表現も頑張って訓練しておく。
Feature Representation
特徴の表現は以下のようにつくる。
- 重心を原点に置くように平行移動させる。
- 回転や変換が加われば、特徴ベクトルもそれを認識して変わるようなエンコーダーを考える。
- 単純に2Dでも3Dでもピースをハメるのではなく正しい向きにして合わせる必要がある。
Diffusion Models for Reassembly Tasks
座標と回転について、結合した新たなベクトルを考える。このベクトルにだんだんとノイズを加えて向きや座標を壊していく。
Forward Process
OU過程の順過程は以下のようになる。
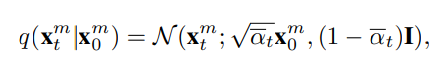
Backward Process
OU過程の逆過程は以下のようになる。
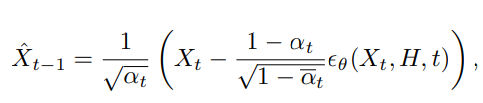
学習について
一般的なDDPMでは、の状態を損失関数に入れるのはなく、最初に戻したの状態だけ予測する。
損失について
位置ベクトルと回転行列についてそれぞれ別々の損失を考えた。
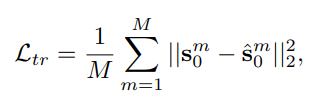
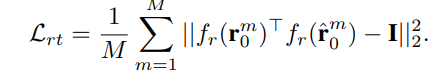
使うGNNの構造について
UniMPのL層にAttentionするGNNを使うらしい。
GNNは隣接するノードに情報を伝搬させて、特徴ベクトルを更新し合う。(一般的には完全グラフを使う)
UniMP(Unified Message Passing)は、複数のheadでAttentionを行い、
Experiments